Unidad I. Ángulos entre rectas paralelas cortadas por una secante (Utilizando Geogebra).
Ángulos entre paralelas cortadas por una secante (Utilizando GeoGebra)
Ángulos entre rectas paralelas y una secante: en geometría son los ocho ángulos formados por dos rectas paralelas y una transversal a ellas. Estableciendo una relación a distancia entre los ángulos que son formados.

Competencias especificas:
- Razona y argumenta: Distingue las nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad.
- Identifica y construye ángulos: correspondientes, alternos internos, alternos externos y opuestos por el vértice.
- Identifica las propiedades de los diferentes tipos de ángulos estudiados y las aplica en la resolución de problemas.
- Comunica: Usa la simbología propia de ángulos, pares ordenados, y las diferentes posiciones de dos o más rectas.
- Modela y representa: Representa con lenguaje matemático y gráficamente segmentos y diferentes ángulos estudiados, pares ordenados y figuras geométricas en GeoGebra.
- Realiza construcciones de ángulos.
- Resuelve problemas: Resuelve problemas para cuya solución se apliquen las diferentes propiedades y relaciones existentes entre los ángulos alternos internos, ángulos alternos externos, ángulos correspondientes y ángulos opuestos por el vértice.
- Utiliza herramientas tecnológicas: Construye rectas perpendiculares, paralelas, bisectrices de ángulos, usando instrumentos apropiados o dispositivos electrónicos.
Indicadores de logros:
Al finalizar esta actividad el estudiante será capaz de:- Estimar de forma aproximada medidas de segmentos y de ángulos dados y las verifica con la ayuda de GeoGebra.
- Estimar de forma aproximada medidas de ángulos dados y las verifica con GeoGebra.
- Realizar el cálculo mental de la medida del complemento y suplemento de un ángulo, en grados, minutos y segundos.
- Construir rectas paralelas y perpendiculares, bisectriz de un ángulo y mediatriz de un segmento utilizando GeoGebra.
- Identificar puntos del plano dados sus pares ordenados (abscisa, ordenada) de números enteros y fraccionarios usando papel cuadriculado.
- Identificar ángulos: correspondientes, alternos internos, alternos externos y opuestos por el vértice.
-Indicaciones para el lector:
Bienvenidos nuevamente a nuestro blog educativo, dentro hay distintas actividades las cuales ayudarán a que los estudiantes aprendan y poner en práctica el concepto: Ángulos entre paralelas.
Actividades:
Para comenzar con esta hermosa unidad hagamos un pequeño repaso sobre los ángulos y sus tipos, en la siguiente página interactiva encontrarás lo que debes hacer. Además pueden auxiliarse del siguiente video.

- Nombre de la actividad: Dulce de paralelas cortadas.
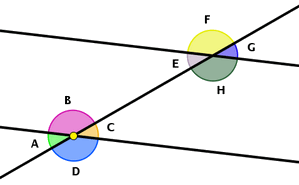
- ¿Cuáles son los pares de ángulos opuestos por el vértice? ¿Qué relación guardan entre sí los ángulos opuestos por el vértice? Cambia la posición de las rectas y repite la medición. ¿Se mantiene la relación entre ambos?
- ¿Qué pares de ángulos adyacentes observas? ¿Qué relación guardan entre sí los ángulos adyacentes? Cambia la posición de las rectas y repite la medición. ¿Se mantiene la relación entre ambos?
- Mueve las rectas para que el ángulo C mida 37º. ¿Cuánto miden los demás ángulos?
- Señala todas las parejas de ángulos correspondientes que veas. ¿Qué relación guardan entre sí dos ángulos correspondientes? Cambia ahora la posición de las rectas (mueve alguno de los puntos). ¿Se mantiene la relación que has encontrado? Haz una captura de pantalla y señala en él las parejas de ángulos correspondientes.
- Señala todas las parejas de ángulos alternos internos que veas. ¿Qué relación mantienen entre sí dos ángulos alternos internos? Cambia ahora la posición de las rectas (mueve alguno de los puntos). ¿Se mantiene la relación que has encontrado? Haz las mediciones oportunas y compruébalo. En la captura hecha anteriormente señala en él las parejas de ángulos alternos internos.
- Señala todas las parejas de ángulos alternos externos que veas. ¿Qué relación mantienen entre sí dos ángulos alternos externos? Cambia ahora la posición de las rectas (mueve alguno de los puntos). ¿Se mantiene la relación que has encontrado?
- Mueve las rectas para que el ángulo C mida 42º. ¿Cuánto miden los demás ángulos? Haz tus cálculos a partir de las relaciones que has encontrado en los apartados anteriores.
- Mueve ahora las rectas para que el ángulo H mida 64º. ¿Cuánto miden los demás ángulos? Haz tus cálculos a partir de las relaciones que has encontrado en los apartados anteriores.
- ¿Puedes conseguir que los 8 ángulos sean iguales? ¿Cuál será su valor en ese caso? ¿Por qu




Comentarios
Publicar un comentario